Structural study of Na8[AlSiO4]6(CO3)2(H2O)4 sodalite: Order and disorder of carbonate anions in sodalite
The sodalite structure can be described by the space-filling array of a [4668]-truncated octahedron known as sodalite or ![]() -cage. Each cage contains guest constituents like four water molecules or cation/anion pairs. If there are monovalent anions (X) inside the sodalite, each cage contains one anion in the centre and four sodium cations at sites close to the six ring openings, forming a tetrahedron. The formula unit Na8[AlSiO4]6X2 contains a total of two cages. Thereby on a total ordering of silicon and aluminium atoms in the framework the cubic space group is P
-cage. Each cage contains guest constituents like four water molecules or cation/anion pairs. If there are monovalent anions (X) inside the sodalite, each cage contains one anion in the centre and four sodium cations at sites close to the six ring openings, forming a tetrahedron. The formula unit Na8[AlSiO4]6X2 contains a total of two cages. Thereby on a total ordering of silicon and aluminium atoms in the framework the cubic space group is P![]() 3n. If divalent anions like carbonate (CO32-) are present, only every second cage is occupied by one anion with the sum formula Na8[AlSiO4]6X. Here the question of order and disorder of the templates has to be discussed:
3n. If divalent anions like carbonate (CO32-) are present, only every second cage is occupied by one anion with the sum formula Na8[AlSiO4]6X. Here the question of order and disorder of the templates has to be discussed:
- (i)
- If the anions are placed in a strong alternating order over the whole structure the space group symmetry is P23. Sodalites with ordered divalent guest anions can be called "noseans".
- (ii)
- If the anions are distributed randomly over the whole structure, an average structure is the consequence and the cubic space group should be P
 3n as in the case of monovalent anions.
3n as in the case of monovalent anions.
Up to now several structure investigations were performed on the question of ordered or disordered distribution of sulphate in natural nosean and was discussed in a controversial manner. Machatschki [8] proposed a statistical distribution of sulphate in the structure, just like Hassan & Grundy [9] who performed structure refinements in the high symmetry space group P![]() 3n. Additional reflexes give rise to the existence of antiphase domain boundaries. The spacegroup of each domain is P23, a sub group symmetry of P
3n. Additional reflexes give rise to the existence of antiphase domain boundaries. The spacegroup of each domain is P23, a sub group symmetry of P![]() 3n. Other authors [10, 11] recommended a total ordering and a lower space group symmetry.
3n. Other authors [10, 11] recommended a total ordering and a lower space group symmetry.
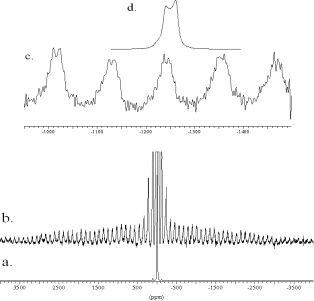
From the 23Na Satellite Transition Spectroscopy (SATRAS) NMR spectrum of hydrated carbonate sodalite Na8[AlSiO4]6(CO3)2(H2O)4 in Figure 3 arises that the resonance consists of two signal parts: a small component with a low quadrupolar coupling constant of CQ = 0.2 ![]() 0.1 MHz and a line shape of second order with CQ = 1.7
0.1 MHz and a line shape of second order with CQ = 1.7 ![]() 0.8 MHz. Figure 3b depicts an expanded plot of the SATRAS spectrum. The quadrupolar coupling constants can be calculated from the difference of the centre of gravity of the central transition and the satellite transition [12]. The centre bands of the satellite transition are usually hidden by the central transition, but can be easily determined by the average position of two symmetrically displaced side bands located at
0.8 MHz. Figure 3b depicts an expanded plot of the SATRAS spectrum. The quadrupolar coupling constants can be calculated from the difference of the centre of gravity of the central transition and the satellite transition [12]. The centre bands of the satellite transition are usually hidden by the central transition, but can be easily determined by the average position of two symmetrically displaced side bands located at ![]() n
n![]() [13]. The large standard deviation of the estimated quadrupolar coupling constant of the latter signal is caused by the large line width of the outer spinning side bands of about 40 ppm. The quadrupolar pattern of the central transition reappears (Figure 3d) as a mirror image in the outer spinning side bands of the satellite transition (Figure 3c) [12]. The satellite transition side bands of the lorentzian signal cover only a frequency scale of
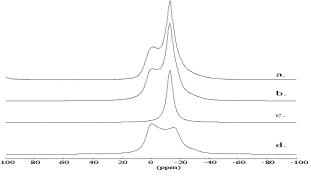
[13]. The large standard deviation of the estimated quadrupolar coupling constant of the latter signal is caused by the large line width of the outer spinning side bands of about 40 ppm. The quadrupolar pattern of the central transition reappears (Figure 3d) as a mirror image in the outer spinning side bands of the satellite transition (Figure 3c) [12]. The satellite transition side bands of the lorentzian signal cover only a frequency scale of ![]() 100 KHz and so only the quadrupolar pattern contributes to the intensity of the outer spinning side bands. Thus the 23Na MAS line shape (Figure 4) of the central transition can be simulated by a lorentzian line with its centre of gravity at -13.0 ppm (component c) and a quadrupolar pattern with
100 KHz and so only the quadrupolar pattern contributes to the intensity of the outer spinning side bands. Thus the 23Na MAS line shape (Figure 4) of the central transition can be simulated by a lorentzian line with its centre of gravity at -13.0 ppm (component c) and a quadrupolar pattern with ![]() = 7.6
= 7.6 ![]() 0.1 ppm, CQ = 2.68
0.1 ppm, CQ = 2.68 ![]() 0.05 MHz and
0.05 MHz and ![]() = 0.2
= 0.2 ![]() 0.1 (component d). The ratio of areas is 30:70. The two resonances result from two different local sodium environments. Half of all cages is filled with 4 water molecules while the other half is filled up with one carbonate anion. The lorentzian signal results from the sodium coordinated by water which experiences a low quadrupolar interaction. The quadrupolar pattern is due to the carbonate filled cages.
0.1 (component d). The ratio of areas is 30:70. The two resonances result from two different local sodium environments. Half of all cages is filled with 4 water molecules while the other half is filled up with one carbonate anion. The lorentzian signal results from the sodium coordinated by water which experiences a low quadrupolar interaction. The quadrupolar pattern is due to the carbonate filled cages.
A calculation of the quadrupolar interaction of sodium coordinated by carbonate using the point charge model of Koller et al. [14] was carried out. The atomic coordinates of oxygen and sodium located in the carbonate filled cages were token from the Rietveld refinement discussed below and the bond valence model of Brown et al. [15, 16] was applied for estimation of oxygen charges. The calculation reveals a quadrupolar coupling constant of CQ = 2.82 ![]() 0.44 MHz, an asymmetry parameter of
0.44 MHz, an asymmetry parameter of ![]() = 0.0
= 0.0 ![]() 0.1, and an isotropic shift of
0.1, and an isotropic shift of ![]() =1.5
=1.5 ![]() 4.1 ppm. These results are in good agreement with the experimental values and support the assignment. Surprisingly the ratio of areas is 30:70 and not 50:50 as expected. Normally every cage should be occupied by four sodium cations. Nevertheless the ratio of areas obtained from the 23Na MAS NMR fit gives evidence for the residence of additional sodium inside the carbonate filled cages as a reason of charge balance. The correctness of this presumption can be proved by Rietveld.
4.1 ppm. These results are in good agreement with the experimental values and support the assignment. Surprisingly the ratio of areas is 30:70 and not 50:50 as expected. Normally every cage should be occupied by four sodium cations. Nevertheless the ratio of areas obtained from the 23Na MAS NMR fit gives evidence for the residence of additional sodium inside the carbonate filled cages as a reason of charge balance. The correctness of this presumption can be proved by Rietveld.
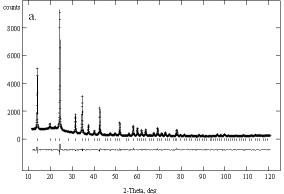
Finally, Rietveld structure refinements were carried out for the carbonate sodalite. All refinements were carried out with the GSAS program package [17]. The sodalite was dehydrated at 673 K and then filled into a closed capillary for data collection. The strong 001- reflex is inconsistent with space group P![]() 3n and gives rise to a lower symmetry. As described by Hassan & Grundy [9] the P
3n and gives rise to a lower symmetry. As described by Hassan & Grundy [9] the P![]() 3n subgroup symmetry P23 should be right to carry out the structure refinement. The question of full or partial order of carbonate over the structure has to be discussed now. The starting atomic positions were taken from the literature [18]. Silicon (Si(1)) and aluminium (Al(1)) were set on Wyckoff position 6g and 6h. Two different framework oxygen (O(1) and O(2)) have to be placed on general position 12j due to the different cage sizes of the dehydrated sodalite. The carbonate carbon atom (C(1) and C(2)) was placed in the centre of each cage on Wyckoff position 1a and 1b with a starting occupancy of 1/2. The carbonate oxygen (OC(1) and OC(2)) were placed on general position 12j (0.060, 0.948, 0.111) and (x + 1/2, y + 1/2, z + 1/2), which contains a 12-fold disorder of the anion in each cage. Soft constraints were set for bond length (1.30 Å
3n subgroup symmetry P23 should be right to carry out the structure refinement. The question of full or partial order of carbonate over the structure has to be discussed now. The starting atomic positions were taken from the literature [18]. Silicon (Si(1)) and aluminium (Al(1)) were set on Wyckoff position 6g and 6h. Two different framework oxygen (O(1) and O(2)) have to be placed on general position 12j due to the different cage sizes of the dehydrated sodalite. The carbonate carbon atom (C(1) and C(2)) was placed in the centre of each cage on Wyckoff position 1a and 1b with a starting occupancy of 1/2. The carbonate oxygen (OC(1) and OC(2)) were placed on general position 12j (0.060, 0.948, 0.111) and (x + 1/2, y + 1/2, z + 1/2), which contains a 12-fold disorder of the anion in each cage. Soft constraints were set for bond length (1.30 Å ![]() 0.05 Å) and bond angles (120
0.05 Å) and bond angles (120![]() 2
2![]() ). Three sodium positions were placed on Wyckoff position 4e (0.195, x, x), (0.8, x, x) and (0.7, x, x). These positions can be detected clearly by Difference Fourier synthesis after a first refinement of the framework atoms. The occupancies were set to 1/3. In following cycles the occupancies of Na, C, and OC were refined, whereas the occupancies of C(1) and OC(1) as well as C(2) and OC(2) were constrained by the factor 1/4. It was noticed that occupancies of C(2) and OC(2) shifted against zero. Therefore full order of carbonate inside the structure can be assumed and C(2) and OC(2) were removed from the refinement. In last cycles the displacement parameters of Si(1) and Al(1), O(1) and O(2) were constrained and all displacement parameters refined.
). Three sodium positions were placed on Wyckoff position 4e (0.195, x, x), (0.8, x, x) and (0.7, x, x). These positions can be detected clearly by Difference Fourier synthesis after a first refinement of the framework atoms. The occupancies were set to 1/3. In following cycles the occupancies of Na, C, and OC were refined, whereas the occupancies of C(1) and OC(1) as well as C(2) and OC(2) were constrained by the factor 1/4. It was noticed that occupancies of C(2) and OC(2) shifted against zero. Therefore full order of carbonate inside the structure can be assumed and C(2) and OC(2) were removed from the refinement. In last cycles the displacement parameters of Si(1) and Al(1), O(1) and O(2) were constrained and all displacement parameters refined.
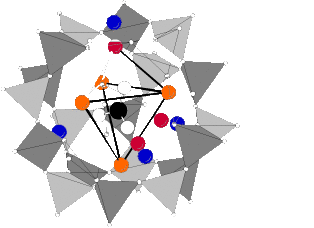
The refinement converged with Rwp = 0.0359, Rp = 0.0247 and R(F2) = 0.03681. It is conspicuous that carbonate is principally coordinated by two sodium sites: Na(1) with a distance of 2.77 Å and 2.74 Å and Na(3) with a distance of 2.37 Å respectively. These results are very similar to results of Sieger et al. [18] who refined a pure formate sodalite after calcination and found a third sodium position, too. In addition the half width of the 001-reflex is about a third larger than that of all other reflexes. A formation of domain boundaries during calcination could be an explanation. For optimization of charge balance one-half of the sodium cations of the free cage are located partially in the carbonate containing cages as depicted in Figure 6. This is in contrast to the refinement of Sieger et al. [18] who assumed a quarter of sodium cations of the free cages are located temporarily in the carbonate cage. However they did not refine the subsequent occupancies. Additionally the 23Na MAS line shape of the hydrated calcined product gives evidence for that assumption. 70 % of the sodium cations are coordinated by carbonate and only 30 % by water (Figure 4)
Hence, there is considerable evidence that carbonate is coordinated by additional sodium from the neighbouring cages even in the hydrated calcined sample but no clear proof.
To examine the question a final structure refinement of the hydrated calcined product was carried out. The starting parameters were taken from the refinement of the dehydrated calcined sodalite and an additional oxygen OH1 due to water was placed on position 4e (0.38, x, x). Occupancies of Na and OH1 as well as the atomic parameters and the displacement parameters were refined. Constraints were set as in the refinement of the dehydrated sample. The refinement converged with Rwp = 0.0345, Rp = 0.0258 and R(F2) = 0.0386. The powder pattern, the Bragg positions and the difference pattern are depicted in Figure 52. It can be seen that the ratio of sodium coordinated by carbonate to sodium coordinated by water is 72:28 and is in agreement with corresponding areas from the 23Na MAS NMR spectrum [19]. The arrangement of the carbonate ion and the coordination two sodium ions is shown in Figure 6


