Seminar "Komplexe Geometrie"
Future talks:
|
E. Faber (Toronto - |
Fr. 18 jul. 2014, 14:15-16:00, Raum NA 4/24 |
| Resolution of singularities and non-commutative rings. Show/Hide summary | |
Motivated by algebraic geometry, one studies non-commutative analogs of resolutions of singularities. In short, non-commutative resolutions of commutative rings
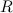 are endomorphism rings of certain are endomorphism rings of certain 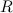 -modules of finite global dimension. However, it is not clear which values of finite global dimensions are possible, even for rings of low Krull-dimension. This leads us to consider the so-called global spectrum of a ring -modules of finite global dimension. However, it is not clear which values of finite global dimensions are possible, even for rings of low Krull-dimension. This leads us to consider the so-called global spectrum of a ring 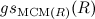 , the set of all possible global dimensions of endomorphism rings of Cohen-Macaulay-modules. When , the set of all possible global dimensions of endomorphism rings of Cohen-Macaulay-modules. When 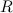 is artinian and is artinian and 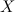 is the category of modules which are both generator and cogenerator, then the minimum value in is the category of modules which are both generator and cogenerator, then the minimum value in 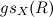 has been studied as representation dimension of has been studied as representation dimension of 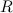 (initiated by M. Auslander).
In this talk we discuss several approaches to non-commutative resolutions, in particular Van den Bergh's non-commutative crepant resolution and the approach of Dao-Iyama-Takahashi-Vial. Then we study their relevance for non-normal rings, in particular the question, under which conditions a non-commutative resolution exists. We will address some questions connected with the global spectrum and discuss several examples coming from algebraic geometry. This is joint work with H. Dao and C. Ingalls. (initiated by M. Auslander).
In this talk we discuss several approaches to non-commutative resolutions, in particular Van den Bergh's non-commutative crepant resolution and the approach of Dao-Iyama-Takahashi-Vial. Then we study their relevance for non-normal rings, in particular the question, under which conditions a non-commutative resolution exists. We will address some questions connected with the global spectrum and discuss several examples coming from algebraic geometry. This is joint work with H. Dao and C. Ingalls. |
|
Given talks:
| G. Dimitrov (Wien) | Fr. 22 nov. 2013, 13:00-14:00, Raum NA 4/24 |
| Homogeneous hypercomplex structures - Compact Lie groups and their coset spaces Show/Hide summary | |
We introduce a remarkable partially ordered subset "the stem" of the set of positive roots of a reduced root system. Using the stem we answer some questions regarding homogeneous hypercomplex structures. In particular we give a complete list of the compact, simply-connected, homogeneous, hypercomplex spaces. This is a joint work with Vasil Tsanov.
|
|
|
A. Ghigi (Bonn - |
Fr. 29 nov. 2013, 14:00-16:00, Raum NA 4/24 |
| Momentum maps and measures on Kähler manifolds Show/Hide summary | |
Let M be a Kähler manifold with a Hamiltonian action of a compact group K. Let G denote the complexification of K. Then G acts on the set of smooth measures on M. This action can be lifted to a Hamiltonian action on an infinite dimensional Kähler manifold X that
fibers over the set of smooth measures. I will show that the orbits of G always intersect the zero set of the momentum map. In the case of flag
manifolds this recovers known results that were proved by different methods.
|
|
| A. Marzouki (Nancy) | Fr. 06 dec. 2013, 14:00-16:00, Raum NA 4/24 |
| Analysis of the structural continuity in twinned crystals in terms of pseudo-eigensymmetries of crystallographic orbits Show/Hide summary | |
A twinned crystal (twin) is a heterogeneous crystalline edifice composed of two or more homogeneous crystals of the same phase with different orientation related by a twin operation t, i.e. a crystallographic operation mapping the orientation of one individual onto that of the other(s). The heterogeneity of twins forms an obstacle for the structural investigation and the technological applications of the concerned materials (e.g. the piezoelectric effect is reduced or annihilated by the presence of twinning). Our approach allows to obtain a general structural theory of twinning which gives the sufficient conditions for the formation of twins. It is based on the search for non-characteristic crystallographic orbits whose eigensymmetry contains the twin operation t.
|
|
|
H. Seppänen (Göttingen - |
Fr. 13 dec. 2013, 10:00-12:00, Raum NA 4/64 |
| Okounkov bodies for families of line bundles Show/Hide summary | |
|
An Okounkov body Δ(L) of a line bundle L over a complex projective variety X of dimension n is a compact convex set in Rn that carries information about the asymptotics of the section ring R(L) of L.
These bodies depend on a flag of irreducible subvarieties of X. One of the fundamental problems is to find flags of subvarieties which yield polyhedral bodies Δ(L). This question has been settled for ample line bundles L by choosing the varieties in the flag suitably with respect to L. A natural question now is whether a given flag can yield polyhedral Okounkov bodies for some given class of line bundles instead of just a single one. I will discuss approaches to solving this problem. |
|
|
J. Gandini (Göttingen - |
Fr. 17 jan. 2014, 10:15-12:00, Raum NA 4/64 |
| A generalization of the Bruhat Decomposition Show/Hide summary | |
Let G be a connected reductive algebraic group and let B be a Borel subgroup of G, then B acts with finitely many orbits on the flag variety G/B, and the orbits are parametrized by the Weyl group of G. In the talk I will consider the case of a subgroup H of B which still acts on G/B with finitely many orbits, and will explain how to parametrize the H-orbits on G/B. An action of the Weyl group W on the set of H-orbits was defined by Knop, we will give an interpretation of this action in terms of weight polytopes and of the natural action of W on the weight lattice of G. The talk is based on a joint work with Guido Pezzini.
|
|
|
S. Trivedi (Krakow - |
Th. 23 jan. 2014, 16:15-18:00, Raum NA 3/64 |
| Stability of transversality and regularity of stratifications Show/Hide summary | |
I will talk about the stability of transversality of maps transverse to stratifications. A generalization of an old result of Trotman, conjectured in his phd thesis, on Thom regularity of stratified maps will be presented. I will also present an analogue of Trotman's result for holomorphic maps and complex analytic stratifications. The latter requires the notion of Oka manifolds introduced by Forstneric.
|
|
|
L. Battisti (Bochum - |
W. 05 feb. 2014, 12:15-14:00, Raum NA 5/64 |
| What is an OT-manifold? (Part I) Show/Hide summary | |
The goal of this talk is to describe the construction of OT-manifolds, a class of non-Kähler compact complex manifolds constructed by Oeljeklaus and Toma. We will start with recalls on number theory and construct the manifolds.
|
|
|
H. Bergner (Bochum - |
Fr. 07 feb. 2014, 10:15-12:00, Raum NA 4/64 |
| Jordan algebras Show/Hide summary | |
In the talk, I will explain some basic definitions and notions related to Jordan algebras, such as semi-simple and Euclidean
Jordan algebras, automorphism group, structure group and derivations. Time permitting, I will also give a characterization of closed orbits
of the automorphism group of a semi-simple complex Jordan algebra under the diagonal action on the n-fold product of the Jordan algebra, and give an outline of the proof.
|
|
| L. Battisti (Bochum) | Fr. 07 feb. 2014, 12:30-14:00, Raum NA 5/24 |
| What is an OT-manifold? (Part II) Show/Hide summary | |
In this part we will study some of the geometrical properties of OT-manifolds, namely their non-Kählerianity and the existence of Locally conformally Kähler metrics and see how these relate to new problems in number theory. Depending on time, we will also see how to compute their algebraic dimension.
|
|
|
G. Gagliardi (Tübingen - |
Fr. 28 feb. 2014, 10:15-12:00, Raum NA 3/24 |
| Three applications of Cox rings to spherical varieties Show/Hide summary | |
We present three theorems on spherical varieties whose proofs involve the theory of Cox rings: 1) a combinatorial criterion for any two points of a spherical variety being contained in some affine open subset. 2) a combinatorial smoothness criterion for spherical varieties. 3) a description of the homogeneous spherical datum of an orbit in a spherical embedding. The third theorem is joint work with Johannes Hofscheier.
|
|
|
E. Hristova (Bochum - |
W. 12 mar. 2014, 14:15-16:00, Raum NA 2/64 |
| Branching laws for tensor modules over classical locally finite Lie algebras Show/Hide summary | |
Given an embedding g' into g of two Lie algebras and an irreducible g-module M the branching problem is to determine the structure of M as a module over g'. In this talk we consider the case when g' and g are classical locally finite Lie algebras and M is a simple tensor g-module. We will start by introducing the necessary background on locally finite Lie algebras and tensor modules. Then we will describe the solution of the branching problem for triples (g',g,M) as above. In particular, since M is in general not completely reducible as a g'-module, we will determine the socle filtration of M over g'.
|
|
|
M. Ruggiero (Paris - |
Fr. 14 mar. 2014, 14:15-16:00, Raum NA 2/64 |
| Attraction rates for iterates of superattracting germs in dimension 2 Show/Hide summary | |
We show that the sequence of attraction rates for the iterates of a superattracting germ of C² satisfies a suitable linear recurrence relation.
The proof is based on the construction of algebraically stable models for such gerns, and the study of the dynamics induced on the valuative tree.
Joint work with William Gignac.
|
|
|
B. Villa (Bochum - |
W. 19 mar. 2014, 14:15-16:00, Raum NA 3/24 |
| On the convex hull of non-compact Kählerian coadjoint orbits. Show/Hide summary | |
We will study Kählerian coadjoint orbits of hermitian Lie groups. A typical example is given by the real symplectic group. I will present which coadjoint orbits admit a Kählerian structure.
It is known that the momentum image of these orbits onto a compact Cartan subalgebra are convex polyhedra.
The goal of the talk is to understand the structure of the faces of the convex hull of these orbits.
For example we will show that all faces are exposed.
|
|
|
V. Tsanov (Bochum - |
Fr. 11 apr. 2014, 10:15-12:00, Raum NA 4/64 |
| Homogeneous projective varieties with tame secant varieties. Show/Hide summary | |
Let X be a homogeneous projective variety. Then X is the orbit of a highest weight line in an irreducible representation V of a semisimple algebraic group G; also, X is the unique closed G-orbit in P(V). Then X spans V, so every vector v in V is a sum of points in X. The rank of v is the minimal number of summands. The r-th secant variety of X is the Zariski closure of the set points of rank r, a classical object in algebraic geometry. This notion of rank generalises the classical matrix rank. Matrix rank is upper-semicontinuous, and this makes the secant vareities relatively easy to describe and understand. However, upper-semicontinuity fails in general. We classify all homogeneous varieties with upper-semicontinuous rank function; we say in such case that the secant varieties are tame. With the list in hand, one can make a number of observations, compute the ideals of the secant varieties, notice a relation to subminuscule and spherical representations. The understanding of these relations presents an open problem. This is joint work with Alexey Petukhov.
|
|
|
H. Franzen (Wuppertal - |
Fr. 25 apr. 2014, 14:15-16:00, Raum NA 4/24 |
| Chow Groups of Non-Commutative Hilbert Schemes. Show/Hide summary | |
Non-commutative Hilbert schemes are fine moduli spaces which parametrize left ideals of a fixed codimension in a path algebra. We show that the Chow group of a non-commutative Hilbert scheme possesses a basis consisting of monomials in Chern classes of the universal bundle. Moreover, we realize these Chow groups as a quotient of Kontsevich's and Soibelman's Cohomological Hall algebra and give a description of the kernel.
|
|
|
M. Kalus (Bochum - |
Fr. 09 may 2014, 10:15-12:00, Raum NA 4/64 |
| Supermanifolds of low odd dimension. Show/Hide summary | |
Any complex supermanifold is naturally associated to a complex vector bundle
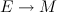 . For a fixed bundle the classification of associated complex supermanifold structures involves the complicated computation of the cohomology of a sheaf of non-abelian groups. The cochains of this cohomology are the deviations of the gluing of coordinate patches from the split case . For a fixed bundle the classification of associated complex supermanifold structures involves the complicated computation of the cohomology of a sheaf of non-abelian groups. The cochains of this cohomology are the deviations of the gluing of coordinate patches from the split case 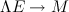 . They appear as the exponential of a . They appear as the exponential of a 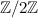 -graded algebra of even nilpotent derivations. Due to this property the difficulty in the classification of supermanifolds increases every second step in odd dimension. Hence reducing the odd dimension of a supermanifold or even better a recipe for increasing the odd dimension is of interest. A method is presented for the lowest dimensional non-abelian case: the step from odd dimension -graded algebra of even nilpotent derivations. Due to this property the difficulty in the classification of supermanifolds increases every second step in odd dimension. Hence reducing the odd dimension of a supermanifold or even better a recipe for increasing the odd dimension is of interest. A method is presented for the lowest dimensional non-abelian case: the step from odd dimension 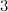 to to 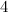 and and 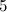 . The talk is planed to be self-contained. . The talk is planed to be self-contained.
|
|
|
G. Schwarz (Brandeis University - |
Fr. 09 may 2014, 14:15-16:00, Raum NA 4/24 |
| An Oka principle for equivariant isomorphisms. Show/Hide summary | |
Let
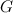 be a reductive complex Lie group and let be a reductive complex Lie group and let 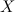 and and 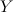 be Stein be Stein 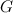 -manifolds. We assume that -manifolds. We assume that 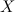 and and 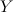 have the same categorical quotient have the same categorical quotient 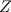 with quotient mappings with quotient mappings 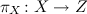 and and 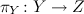 . We also assume that there is an open cover . We also assume that there is an open cover 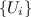 of of 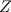 and and 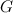 -equivariant biholomorphic mappings -equivariant biholomorphic mappings 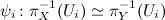 inducing the identity on inducing the identity on 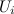 . We establish the following Oka principle: The obstruction to the existence of a . We establish the following Oka principle: The obstruction to the existence of a 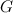 -equivariant biholomorphism -equivariant biholomorphism 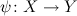 is topological. The obstruction vanishes if and only if there is a special type of equivariant homeomorphism of is topological. The obstruction vanishes if and only if there is a special type of equivariant homeomorphism of 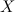 and and 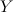 . . |
|
|
J. Torres (Köln - |
W. 14 may 2014, 10:15-12:00, Raum NA 4/64 |
| The symplectic Plactic Monoid and MV Cycles: Paths and Cells in Bott-Samelson varieties. Show/Hide summary | |
We introduce Bott-Samelson varieties as resolutions of singularities of Schubert varieties and describe a general method of obtaining cell decompositions of them, using retractions in the associated building. Then we do this for generalised Schubert varieties in the affine Grassmannian and view fixed points in cells as galleries in the affine building, which in turn are naturally paths in the real form of the coroot lattice. Our results extend results obtained by Gaussent-Littelmann, who associate an MV cycle to certain "LS" galleries by projecting the corresponding cell and taking the closure. Plactic monoids play a role since this association respects the crystal structures dened on galleries (or paths) and MV cycles.
|
|
|
M. Pevzner (Reims - |
Fr. 06 jun. 2014, 10:15-12:00, Raum NA 4/64 |
| Differential symmetry breaking operators. Show/Hide summary | |
We consider the general problem to find explicit formulas for differential
symmetry breaking operators in the setting of multiplicity-free branching laws for
reductive symmetric pairs. For this purpose we develop a new method based on an algebraic
Fourier transform for generalized Verma modules, which enables us to characterize those
intertwining operators by means of certain systems of partial differential
equations of second order.
We illustrate this idea by addressing the problem in the six different complex geometries
arising from real symmetric pairs of split rank one.
|
|
|
L. Kamenova (Stony Brook - New York - |
Fr. 06 jun. 2014, 14:15-16:00, Raum NA 4/24 |
| Kobayashi pseudometric and non-hyperbolicity of hyperkähler manifolds. Show/Hide summary | |
The Kobayashi pseudometric on a complex manifold M is the maximal
pseudometric such that any holomorphic map from the Poincare disk to M is
distance-decreasing. Kobayashi has conjectured that this pseudometric
vanishes on Calabi-Yau manifolds. Using ergodicity of complex structures,
we prove Kobayashi's conjecture for any hyperkähler manifold that admits
a deformation with a Lagrangian fibration, if its Picard rank is not
maximal. We shall discuss the proof of Kobayashi's conjecture for K3
surfaces and for certain hyperkähler manifolds. These results are joint
with S. Lu and M. Verbitsky.
|
|

