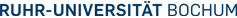Zometool model of a 120 cell

Here we describe how to build a so-called cell-first projection of the 120 cell, one of the six regular polytopes in 4-dimensional space, using the zometool system. For the jumbo model you need

  • 330 balls,
  • 180 long blue (b2) struts,
  • 200 long yellow (y2) struts,
  • 120 long red (r2) struts,
  • 120 middle red (r1) struts.

Of course one can scale down the model to b1-y1-r1-r0 (medium size) or even to b0-y0-r0-r00 (this yields the mini version sold as the Hyperdo kit).

For further information and instructions you might also wish to consult one of the following webpages:

The pictures below were taken by Eva-Maria Gassner.

Step 1


Build a regular dodecahedron using 20 balls and 30 b2 struts. This is the central cell of the projection.


Step 2


Add a lollipop pointing outwards at each of vertex. For this you need 20 balls and 20 y2 struts.



Step 3


Build 30 red bridges using 30 balls and 60 r2 struts. Use them to connect the yellow lollipops constructed in step 2.



Step 4


Build 12 pentagons with outward pointing yellow struts using altogether 60 balls, and 60 b2 and 60 y2 struts. Use them to build 12 squashed dodecahedra on the red bridges constructed in step 3. They form the first layer of our model and show the cells that directly surround the central dodecahedron.



Step 5


Build 30 blue-red bridges using altogether 60 balls, 30 b2 and 60 r1 struts. Erect these bridges over the inward pointing chains of v-shaped yellow struts constructed in step 4.



Step 6


Build 20 yellow-red stars using altogether 80 balls, 120 y2, 60 r2 and 60 r1 struts. These stars are used to connect all the blue-red bridges constructed in step 3. We have now completed the second layer of cells surrounding the central dodecahedron. This second layer consists of 20 squashed and skewed dodecahedra. Moreover, there are some loose red struts that will be connected in the next step.



Step 7


Build 12 blue pentagons and connect them with the loose r1 struts constructed in step 6. This completes the construction of the third layer of 12 dodecahedral cells surrounding the central cell.



The model is now complete. So far we have constructed 1 central cell, 12 cells in the first layer, 20 cells in the second layer and 12 cells in the third layer. However, under the projection from 4d to 3d every cells has two pre-images. This means that in total we have constructed (1+1)+(12+12)+(20+20)+(12+12) = 90 cells. The missing 30 cells can also be seen. Since in 4d they are viewed under a 90 degree angle they appear completely flat in our model and are located on its outer hull.

Only from a certain distance one can see (and appreciate) all its beautiful symmetries.